CHAPTER 2: CONCEPT OF SET

Computer Representation of Sets

There are various methods to represent sets using a computer. There are:

Store the elements of the set in an unordered fashion.
Store the elements using an arbitrary ordering of the elements of the universal set.

a. Store the elements of the set in an unordered fashion:

There would be a time-consuming when the operations of computing the union, intersection, or difference of two sets because each of these operations would require a large amount of searching for elements. So, we will present a method for:

b. Store the elements using an arbitrary ordering of the elements of the universal set.

- This method makes computing combinations of sets easy.

1. Let's assume that set U is a finite and of reasonable size.

2. First, we'll specify an arbitrary ordering of elements of U, for instance a₁, a₂, a₃, ..., a_n.

3. Then, we'll represent a subset A of U with the bit string of length n, where the i th bit in this string is:

if a_i ∈ A, and 0, if a_i ∉ A.

h Example 1:

Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, and the ordering of elements of U has the elements in increasing order; that is, a_i = i . What bit strings represent the subset of all odd integers in U, the subset of all even integers in U, and the subset of integers not exceeding 5 in U?

Solution:

The bit string that represents the set of odd integers in U, namely, {1, 3, 5, 7, 9}, has a one bit in the ﬁrst, third, ﬁfth, seventh, and ninth positions, and a zero elsewhere. It is

10 1010 1010.

Similarly, we represent the subset of all even integers in U, namely, {2, 4, 6, 8, 10}, by the string

01 0101 0101.

The set of all integers in U that do not exceed 5, namely, {1, 2, 3, 4, 5}, is represented by the

String

11 1110 0000.

Example 2:

Let U = {0,1,2,3,4,5,6,7}, A = {1,3,5,6,7}, B = {0,1,2,3,4,5}.

Use bit strings to find

1) Ā (Complement)

Solution:

Bit string for A: 0101 0111,

Then Ā = 1010 1000

(Therefore, Ā = {0,1,2,4})

2) A ∩ B (Intersection)

Solution:

Bit string for A: 0101 0111

Bit string for B: 1111 1100

Then A ∩ B =0101 0111 ˄ 1111 1100 = 0101 0100

(A ∩ B = {1,3,5} )

3) A U B (Union)

Solution:

Bit string for A: 0101 0111

Bit string for B: 1111 1100

Then A U B = 0101 0111 ˅ 1111 1100 = 1111 1111

(A U B = U = {0,1,2,3,4,5,6,7})

The concept of relations between 2 sets
A binary relation from A to B is a subset of A X B
Notation that can be use :
  a R b
  (a, b) ∈ R

    a is said to be related to b by R

Relation Representation
Use the appropriate methods for representing relation:

Using matrices

Using digraphs

The properties of relations

Reflexive Relations

Definition: Binary relation α on a set of A if a α a for every element of A.

Examples:

The relation ≤ is reflexive on R because the statement " r ≤ r" is true for every real number r.
The equals is the relation of reflexive on any set.The Statement "X = X" is true for every mathematical object X.
The relation ⊆ on the power set of any set is reflexive.

Symmetric Relations

Definition:A binary relation α on a set A is symmetric if a α b implies b α a for all element a and b of A.

Examples:

The empty relation is symmetric, because the statement “if a α b then b α a ” is vacuously true.
The equals relation is symmetric. Must show that if a = b, then b = a. But you have known that for years.)
Any nearness relation is symmetric.

Antisymmetric Relations

Definition:

A binary relation α on a set A is antisymmetric if for all elements a, b∈ A, if a α b, b α a.Then a=b.

Examples:

The empty relation is vacuously antisymmetric.
The < relation is vacuously antisymmetric.

Transitive Relations

Definition:

A binary relation α on a set A is transitive if for all elements a, b, and c of A, if a α b and b α c, then a α c.

Examples

The empty relation is vacuously transitive on any set.
The equals relation is transitive on any set. (If a = b and b = c then a = c. This is equivalent to the property given by “two things equal to the same thing are equal to each other.”)
All these relations are transitive on R: >, ≤,,...In general, anything you could call an ordering is transitive.

Functions

Definition : A function f from a set X to a set Y is a relation between the elements of X (called the inputs) and the elements of Y(called the outputs) with the property that each input is related to one and only one output.

We use the notation: f : X → Y

to denote a function from X to Y and we call X the domain of f and

Y the codomain of f.

Given an input x ∈ X of a function f : X → Y , by definition, there is a unique output element y ∈ Y related to x. We say that “f sends x to y” and write x 7→ y or f : x 7→ y. The element
y is usually denoted by f(x) and is called:

• f of x
• the output of f for the input x
• the value of f at x
• the image of x under f

The set of all values of f is called the range of f, or the image of X

under f. Symbolically,

range of f = image of X under f = {y ∈ Y |y = f(x) for some x ∈ X}

Given an element y ∈ Y , an element x ∈ X with f(x) = y is called a preimage of y or an inverse image of y. The set of all inverse images of y is called the inverse image of y. Symbolically, inverse image of y = {x ∈ X|f(x) = y}

Boolean Functions

Definition :is a function f from the Cartesian product ×n{0, 1} to {0, 1}. Alternatively, we write f : ×n{0, 1} → {0, 1}. The set ×n{0, 1}, by definition, the set of all n-tuples (x1, · · · , xn) where each xi is either 0 or 1, is called the domain of f. The set {0, 1} is called the codomain (or, sometimes, range) of f. The Cartesian product ×n{0, 1} is also written {0, 1}n. This corresponds to writing the product of n copies of y as yn.

Example:
Find the values of Boolean function (of degree 3) F(x, y, z) = xy + z.

A Boolean function of degree n can be represented by an n-cube (hypercube) with the corresponding function value at each vertex.

Example:
Express the Boolean function F(x, y, z) = xy + z by a hypercube.

Types of functions

•Injective (one-to-one) :

–Any value in codomain can be produced by at most one value at domain.

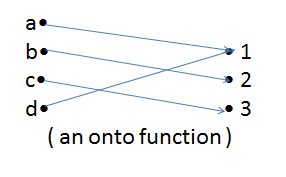
•Surjective (onto) :

–Every value in codomain can be produced by domain.

•Bijective (injective and surjective) :

–Both one-to-one function and onto

Definition of inverse function

Definition: INVERSE OF A FUNCTION: The relation formed when the independent variable is exchanged with the dependent variable in a given relation. (This inverse may NOT be a function.)

Definition: INVERSE FUNCTION: If the above mentioned inverse of a function is itself a function, it is then called an inverse function.

Example :
Find the inverse of y= x^2 + 1, and determine whether the inverse is a function.

Since this passes the Horizontal Line Test, I know that its inverse will be a function. And since this graph is different from that of the previous function, I know that the inverse must be different. Again, it is very helpful to first find the domains and ranges. The function's domain is x > 0; the range (from the graph) is y > 1. Then the inverse's domain will be x > 1 and the range will be y > 0.

Here's the algebra:

Example:

Find the inverse of y = ^–2 / _{(x – 5)}, and determine whether the inverse is also a function.

Since the variable is in the denominator, this is a rational function. Here's the algebra:

This is just another rational function. The inverse function is y = ^{(5x – 2)} / _x

Example:
Find the inverse of f(x) = –sqrt(x – 2), x > 2. Determine whether the inverse is also a function, and find the domain and range of the inverse.
The domain restriction comes from the fact that x is inside a square root. Usually I wouldn't bother writing down "x > 2", because I know that x-values less than would give me negatives inside the square root. But the restriction is useful in this case because, together with the graph, it will help me determine the domain and range on the inverse:

The domain is x > 2; the range (from the graph) is y < 0. Then the domain of the inverse will be x < 0; the range will be y > 2.

Here's the algebra:

Then the inverse y = x² + 2 is a function, with domain x < 0 and range y > 2.

Composition Function

Definition:Composition of Functions is the process of combining two functions where one function is performed first and the result of which is substituted in place of each x in the other function.

Let g be a function from the set A to the set B and let f be a function from the set B to the

set C. The composition of the functions f and g, denoted for all a ∈ A by f ◦ g, is deﬁned

by:

(f ◦ g)(a) = f (g(a)).

Example:

Let g be the function from the set {a, b, c} to itself such that g(a) = b, g(b) = c, and g(c) = a.

Let f be the function from the set {a, b, c} to the set {1, 2, 3} such that f(a) = 3, f(b) = 2, and

f(c) = 1. What is the composition of f and g, and what is the composition of g and f ?

Solution:

The composition f ◦ g is deﬁned by (f ◦ g)(a) = f(g(a)) = f(b) = 2, (f ◦ g) (b) = f(g(b)) = f(c) = 1, and (f ◦ g)(c) = f(g(c)) = f(a) = 3.

Note that g ◦ f is not deﬁned, because the range of f is not a subset of the domain of g.

Presentation Chapter2:CONCEPT OF SET

Click this link:

UNISZA-TAF3023 DISCRETE MATHEMATICS-PRESENTATION-2-FORESPEC

Chapter-2-CONCEPT-OF-SET

Way of listing the elements of Sets

A written description

A is the set of calendar months beginning with the letter

List or Roster Method

A= { January, June, July}

Set builder notation

A = { x │x is a calendar month beginning with the letter J}

Example:

Primary colour

C is the set of primary colour

C = { Blue, Red,Yellow}

C = {x│x is a primary colour}

Properties of sets

Sets are inherently unordered:

•No matter what objects a, b, and c denote,
{a,b,c} ={a,c,b} ={b,a,c} = {b,c,a} = {c,a,b} = {c,b,a}.

All elements are distinct (unequal), multiple listings make no difference

•{a,a,b} = {a,b,b} = {a,b} = {a,a,a,a,b,b,b}.

This set contains at most 2 elements

Set membership

Set is an unordered collection of object, the object inside the set, called elements or members.

We use symbol “∈” and “∉” to denote the element of a set.

For example, “a∈A” mean “a” is the element of the set “A”. While “b ∉ A” mean “b” is not the element of set “A”.

Empty Set

There is a special set, that are no element inside it, which called empty set or null set.

There are 2 symbols to denote an empty set, “Ø” and “{ }”.

It's quite interested when these 2 symbols combine together to become “ {Ø} ” .It's not a empty set ,it's called singleton set. Which represent an empty set in a set itself.

Set of numbers

Natural numbers: N ={0, 1, 2, 3,...},

Integers:Z ={...,−2,−1, 0, 1, 2,...},

Positive integers: Z+ ={1, 2, 3,...},

Rational numbers :Q ={p/q | p ∈ Z,q ∈ Z, and q = 0},

Real numbers: R

Positive real numbers :R+,

Complex numbers :C

Set Equality

Deﬁnition: Set Equality Two sets are equal if they are both subsets of one another. The standard notation for equality, = , is used.
Example: {1, 2, 3} = {3, 2, 1} = {1, 1, 2, 3, 2, 2}

Venn Diagram

These are a pictorial representation of sets and a good way to get intuition about (possible)set equalities.
Universal set U= contains all the objects under consideration, is represented by a rectangle.
Inside this rectangle, circles or other geometrical ﬁgures are used to represent sets.

Example Venn Diagram:

Let us say the third set is "Volleyball", which drew, glen and jade play:

Volleyball = {drew, glen, jade}

But let's be more "mathematical" and use a Capital Letter for each set:

S means the set of Soccer players

T means the set of Tennis players

V means the set of Volleyball players

The Venn Diagram is now like this:

Example Venn Diagram:

In a school of 320 students, 85 students are in the band, 200 students are on sports teams, and 60 students participate in both activities. How many students are involved in either band or sports?

25 + 60 + 140 = 225
There are 225 students involved in either band or sports.

Subset

Encounter situations where the elements of one set are also the elements of a second set.

If all the elements of a set A are also elements of a set B, then we say that A is a subset of B, and we write: A ⊆ B

Example:

If A = {2, 4, 6, 8, 10} and B= {even integers}, then A⊆ B

Power Set

• If we have a set {a,b,c}:

• Then a subset of it could be {a} or {b}, or {a,c}, and so on, and {a,b,c} is also a subset of {a,b,c} .

• And the empty set {} is also a subset of {a,b,c}

• In fact, if you list all the subsets of S={a,b,c} you will have the Power Set of {a,b,c}:

• P(S) = { {}, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c} }

Set Operation

Union (∪)

Definition : The union of a collection of sets is the set that contains those elements that are members at least one set in the collection.

The union of two sets is a new set which combines all of the members of both sets (and discards duplicates).
Example : If A = {1, 2, 3} and B = {4, 5} , then A ∪ B = {1, 2, 3, 4, 5}

Intersection (∩)

Definition: The intersection of a collection of sets is the set that contains those element that are members of all the sets in the collection.

The intersection of two sets is a new set which only includes those members present in both sets.

Example: If A = {1, 2, 3} and B = {1, 2, 4, 5} , then A∩B = {1, 2}

Disjoint Set (Æ )

Definition : Intersection of two sets is the empty set.
Example :If A = {1,3,5,7,9} and B = {2,4,6,8,10}, then A∩B =Æ , S

Set difference

The difference of set A to B denoted as A-B is set of those elements that in set b.
A-B={x:x A and xÏB}
Similarly B-A={x:x B and xÏA}
A general A-B ¹ B-A

Example:

If A={a,b,c,d} and B={b,c,d,f} then A-B={a,d} and B-A={e,f}

Set Complimentary

The complementary event A’ is the set of all elements which do not belong to it.

It is often symbolized by A’ or Ø A. All sampling points of a population are either in A or in A'.

And no sample point can be a member of both A and A’.

Characteristics of set

Generalised Union

Generalised Intersection

Cartesian Product

A new set can be constructed by associating every element of one set with every element of another set. The Cartesian product of two sets A and B, denoted by A × B is the set of all ordered pairs (a, b) such that a is a member of A and b is a member of B.

Example:

What is the Cartesian product of A ={1, 2} and B ={a, b, c}?

Solution:

The Cartesian product A × B:

A × B ={(1, a), (1, b), (1, c), (2, a), (2, b), (2,c)}.

*Note that the Cartesian products A × B and B × A are not equal, unless A =∅ or B =∅ (so that A × B =∅)or A = B

Some basic properties of Cartesian products:

•A × ∅ = ∅.

•A × (B ∪ C) = (A × B) ∪ (A × C).

•(A ∪ B) × C = (A × C) ∪ (B × C).

FORESPEC

Pages

FORESPEC TEAM

Blog Archive

Blogroll

About