GRAPH THEORY

GRAPH THEORY

1) Give the definition and example for each of the following term:
 
    a) Euler Path:
        Euler Path is a path that use every edge of a graph exactly once. The starting and ending points need   
        not be the same.

        example:

     

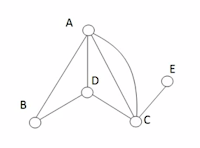
     (E,C,A,C,D,A,B,D)

 

    b) Euler Circuit:
        Euler Circuit is a circuit that use every edge of the graph exactly once. The starting and ending points
        must be the same.
     
         example:

   (D,E,C,B,A,F,D)
 

2) Determine what are the properties that differentiate between (a) and (b) in question 1?
    a) If a graph only vertices of odd degree, then it cannot have on Euler Circuit.
    b) If a graph is connected and and every vertex have even degree, then it has at least one Euler Circuit  
        (usually more).

3) What are the algorithm or step by step to determine (a) and (b) in Question 1?
    a) Make sure the graph has either 0 or 2 odd vertices.
    b) If there are 0 odd vertices, start anywhere. If there are 2 odd vertices, start at one of them.
    c) Follow edges one at a time. If you have a choice between a bridge and non-bridge always choose the
        non-bridge.
    d) Stop when you run out of edges.

4) Give the definition and example for each of the following term:

   a) Hamilton Path:
       Hamilton Path is a path that passes through all the vertices of the graph, each vertex exactly once.

     example:

  G2= (a,b,c,d)

  b) Hamilton Circuit:
      Hamilton Circuit is a circuit that start at one vertex that visits every other vertex in the graph exactly once
      and return to its starting point.

      example:

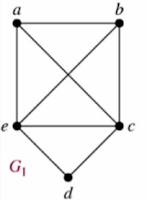
G1= (a,b,c,d,e,a)

5) Determine what are the properties that differentiate between (a) and (b) in Question 4?

    a) Any Hamilton Circuit can be converted to the Hamilton Path by removing one of its edge but a
        Hamilton Path can be extended to Hamilton Circuit only of its ending points are adjacent.

      - Hamilton Circuit:

• n ≥3 vertex
• degree of every vertex is at least n/2
• degree u and v  ≥  n for every pair of nonadjacent  vertices u and v in the graph.

6) What are the algorithm or step by step to determine (a)and (b) in Question 4:

• List edges in increasing order.
• Choose edge of least weight and mark edge.
• Choose next edge of least weight if the edge does not complete a circuit before all vertices have been visited or does not result in 3 marked edges at a vertex.
• Continue step 3 until  Hamilton Circut is form.